1 min read Papers

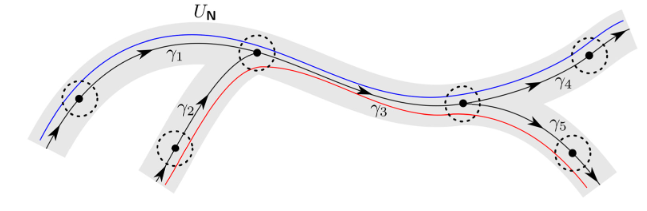
How many points converge to a heteroclinic network in an aperiodic way?

How many points converge to a heteroclinic network in an aperiodic way?
Trajectories near a heteroclinic network, whose equilibria are depicted with black dots. Neighbourhoods of the equilibria are shown as dashed circles. The blue trajectory follows heteroclitic orbits labelled %%\gamma_1%% , %%\gamma_3%%, and %%\gamma_4%%, while the red one follows %%\gamma_2%% , %%\gamma_3%%, and %%\gamma_5%%.

A new article by ACDC member Christian Bick and Alexander Lohse (University of Hamburg, Germany) has just been published on the journal Dynamical Systems. Here is an excerpt from the abstract:

Homoclinic and heteroclinic connections can form cycles and networks in phase space, which organize global phenomena in dynamical systems. On the one hand, stability notions for (omni)cycles give insight into how many initial conditions approach the network along a single given (omni)cycle. On the other hand, the term switching is used to describe situations where there are trajectories that follow any possible sequence of heteroclinic connections along the network. Here we give a notion of asymptotic stability for general sequences along a network of homoclinic and heteroclinic connections. We show that there cannot be uncountably many aperiodic sequences that attract a set with nontrivial measure.