Rigorous integration of parabolic PDEs

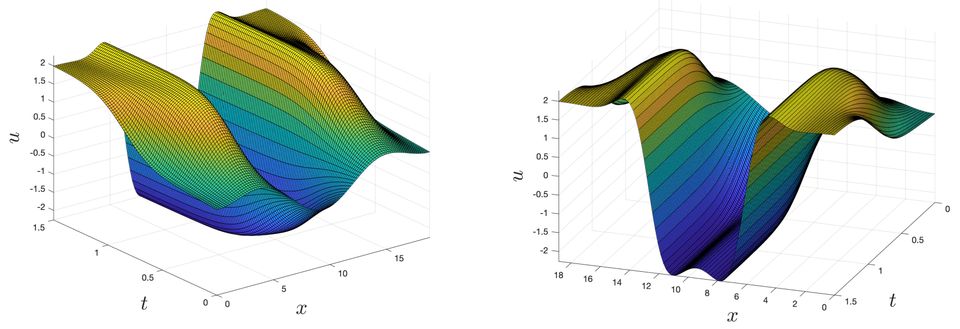
Simulating the dynamics of evolving patterns is at the core of scientific computing. But how reliable are such simulations? In a longrunning collaboration, Maxime Breden (from the Ecole Polytechnique in Paris), Ray Sheombarsing (a VU graduate) and Jan Bouwe van den Berg have developed a method based on functional analysis and rigorous numerics to perform long time integration for semilinear parabolic partial differential equations (PDEs). The flexible code, backed up by theorems in an arXiv preprint, can be applied to various well-known model equations in applied analysis. As an example, the solution of the Swift-Hohenberg equation depicted above is guaranteed to be correct with mathematically verified error bounds of one-in-a-million on the entire space-time domain.