Paper on the two-dimensional suspension bridge equation
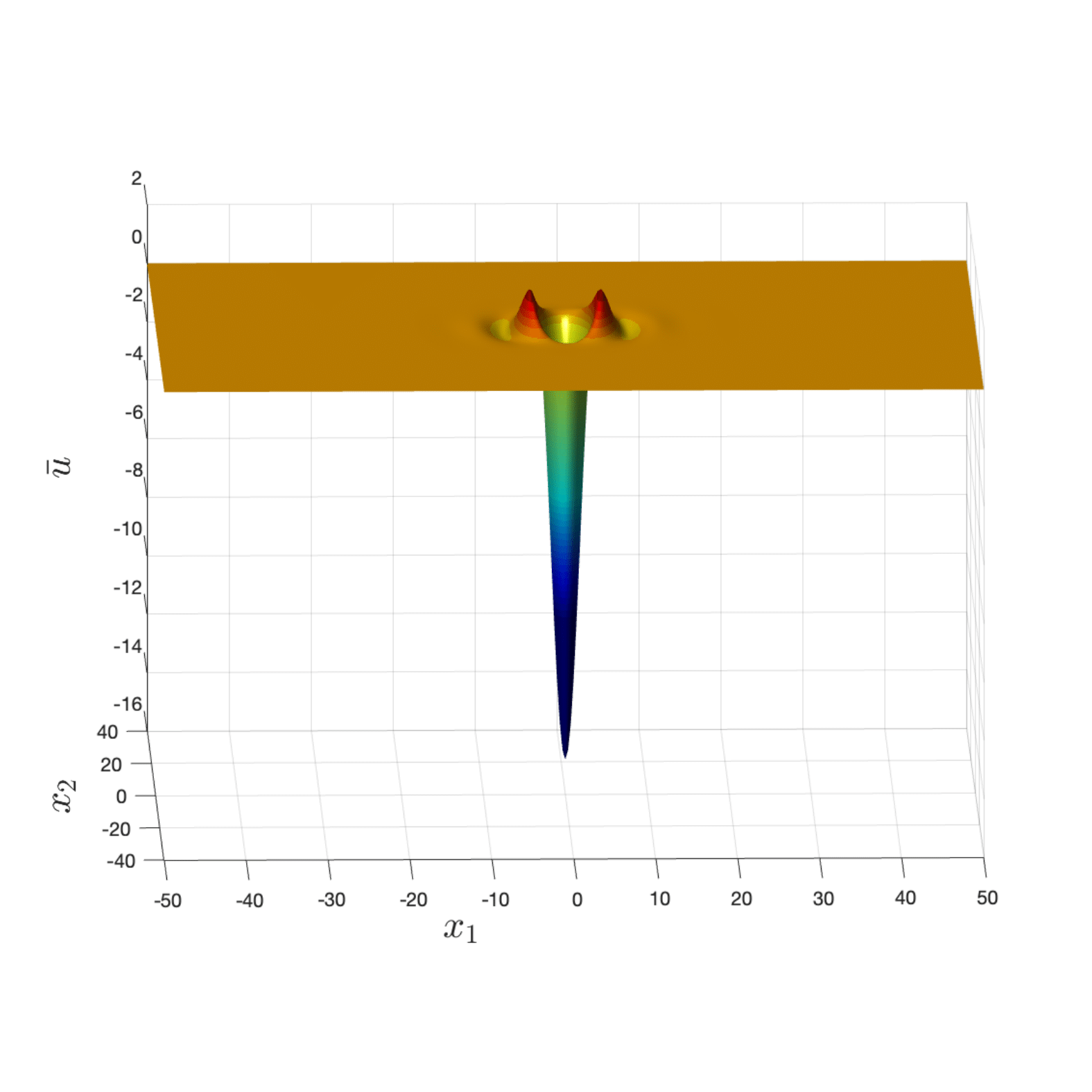
A new paper by Lindsey van der Aalst and Jan Bouwe van den Berg from Vrije Universiteit Amsterdam, and Jean-Philippe Lessard from McGill University (Montreal, Canada), was published on July 9 2025 in Nonlinearity. It establishes the existence of periodic localised traveling wave solutions in the two-dimensional suspension bridge equation. While previous studies have focused mainly on the one-dimensional case, two-dimensional traveling structures have remained largely unexplored beyond numerical simulations. Using computer-assisted proof techniques based on a Newton–Kantorovich type argument, the authors rigorously validate periodic localised waves in two spatial dimensions. The method is readily extendable to a broad class of wave equations and elliptic PDEs with analytic nonlinearities, in both two and higher dimensions.